Il s'agit d'une théorie mathématique, née des travaux d'Erlang (1917) permettant de modéliser les files d'attentes ou queues.
Elle est également utilisée en production. On appelle :
- a : le flux moyen d'arrivée des pièces en amont d'un poste de production (/ unité de temps).
- b: le flux moyen de sortie des pièces en aval du poste de production (/ unité de temps). 1/b est donc le temps de cycle du poste de production = TC.
On appelle ∂ =a/b =a x TC le taux d'utilisation de la capacité de production ou du système (en %), c'est à dire le ratio entre les capacités de production effectivement utilisées pour la production sur l'ensemble des capacités de production de l'entreprise.
L'engorgement est évité uniquement si ∂ < 1 (avec mise en place d'une file d'attente de pièces en aval du système de production).
Si ∂ >= 1, le système est divergent : la file d'attente ne cesse de croître.
Dans les files d'attente M/M/1 (notation de Kendall), caractérisées par un processus d'arrivée obéissant à une loi de Poisson et un seul poste de travail. On appelle "système" l'ensemble formé par le poste de production et la file d'attente.
La probabilité d'avoir k pièces en cours de traitement dans le système est :
p(k) = ∂^k x (1 – ∂)
Dans ces conditions, la théorie des files d'attente donne les relations suivantes :
- le nombre moyen de pièces dans le système (en-cours de production) est égal à :
WIP = ∂ / (1 - ∂)
- le temps moyen d'attente en aval du poste de production (temps de traversée du stock aval) est égal à :
Temps d'attente moyen = (1/b) x ∂ / (1 – ∂) = TC x ∂ / (1 – ∂) = LT x ∂ = TC x WIP
- le temps moyen de séjour dans le système (ou temps de traversée) est égal à :
LT = 1 / (b- a) = TC / (1 – ∂) = WIP / a
Cette dernière relation est connue sous le nom de loi de Little : WIP = LT x a.
On constate que pour un taux d'utilisation faible des capacités de production (∂ proche de 0) LT = TC mais que le temps de traversée augmente fortement lorsque les capacités de production sont saturées (pour ∂= 90%, LT = 10 x TC !).
C'est ainsi qu'en production JAT (juste-à-temps), il est préconisé une légère surcapacité pour réduire les temps de cycle (cf. R. COLIN – "Produire juste à temps en petite série" – p256).
- le nombre moyen de pièces en attente (stock en aval du poste de production ou taille de la file d'attente) est égal à :
I = ∂² / (1 – ∂)
Dans le cadre d'un processus stochastique, caractérisé par une variabilité du processus de production et/ou du flux entrant, cette relation est donnée par la formule d'Allen-Cuneen
I = ∂² / (1 – ∂) x (Centrant²/2 + Cproduction²/2)
avec C = coefficient de variation (écart-type/moyenne) égal à 1 pour une distribution exponentielle.
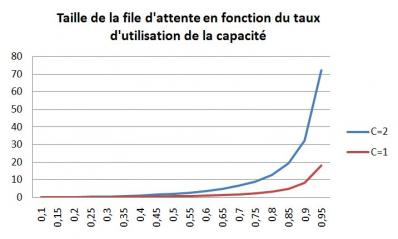
Dans un environnement fortement variable (C =2), il apparait que passer d'un taux d'occupation des ressources de 80 à 85% augmente de moitié la taille des files d'attente et allonge considérablement le temps de traversée de la production. C'est pourquoi, il est préconisé de mettre en place un tampon "ressource" dans ces environnements pour protéger le débit de la survenue d'aléas.
