- Accueil
- Blog
Blog
Le 19/10/2018
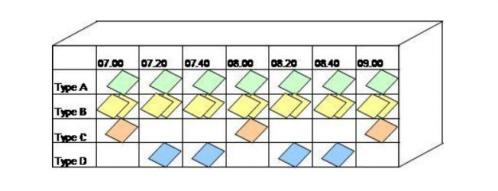
La boîte Heijunka est un outil dont la finalité est de mixer et niveler les ordres de fabrication de plusieurs produits, caractérisés chacun par une forte variabilité des commandes, donc peu propices à la mise en place d’un tableau kanban.
Pour ce faire, on moyenne la production par produit sur une période suffisamment longue pour gommer les pics et les creux, lissant l’objectif de production sur cette période.
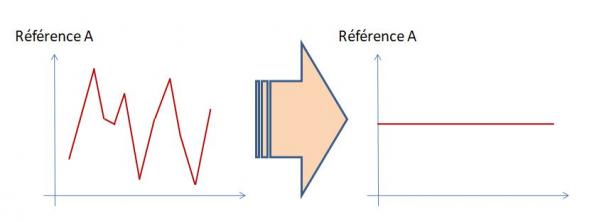
Il s’agit alors de niveler la production en références « produit » et en volumes sur la période couverte par la boîte Heijunka (équipe, journée, semaine,...) afin :
· De réduire l’en-cours (donc les cycles), en diminuant la taille des campagnes de fabrication de chaque référence, et,
· De transmettre aux postes amont une demande régulière en quantité, permettant de réguler les variations de ressources à mettre en œuvre (correspondant à une variation entre le temps requis et le temps requis + quelques heures supplémentaires sans avoir à « embaucher » des personnels de plus).
Elle est particulièrement adaptée en fin de flux, juste avant l’expédition, par exemple sur une opération d’assemblage final (ou l’opération la plus en amont d’un flux continu avant l’expédition).
La boîte Heijunka est souvent associée à un séquenceur permettant de présenter au poste de travail les OF sortis de la boîte Heijunka suivant une logique FIFO :
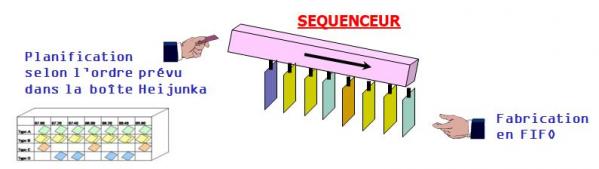
On peut considérer sa mise en œuvre comme un flux tiré par la demande réelle, si les OF pris en compte pour remplir la boîte correspondent à des commandes fermes (ce qui implique que le LT entre l’opération faisant l’objet de la boîte et l’expédition est inférieur au délai de commande).
Une boîte Heijunka est organisée en colonnes représentant une même période de temps (appelée le pitch) et en lignes par famille de produits.
Les temps de cycle de fabrication des produits peuvent être différents ainsi que les temps de changement de série : ainsi, à un pitch peut correspondre un nombre de produits fabriqués différent en fonction de la famille considérée (donc un nombre de cartes [1 carte = 1 container de x pièces] différent dans chaque alvéole de la boîte).
L’agencement des cartes sur la période couverte par la boîte Heijunka (journée, semaine) est revue à chaque début de période en fonction des commandes fermes prévues pour la période suivante : en ce sens, la boîte Heijunka permet d’adapter le profil de production même en cas de forte variabilité de la demande.
Illustrons ceci par deux exemples
EXEMPLE 1 : production avec changement de série
Soit un poste de production ouvert 8h par jour qui fabrique 3 produits A (TC = 1 min), B (TC = 2 min) et C (TC = 5 min). Le temps de changement de fabrication est de 10 minutes. La demande journalière moyenne est la suivante :
· A = 200 soit un temps de production avec C/O de 210 minutes (près de 4h)
· B = 50 soit un temps de production avec C/O de 110 minutes (près de 2h)
· C = 20 soit un temps de production avec C/O de 110 minutes (près de 2h)
Cas 1 : sans nivellement de la production
| Produits | 08h | 09h | 10h | 11h | 13h | 14h | 15h | 16h |
| A = 200 | XXXXXXXXXXXX | |||||||
| B = 50 | XXXXX | |||||||
| C = 20 | XXXXX | |||||||
Les en-cours sont ponctuellement importants et chaque produit n’est délivré qu’une fois par jour.
Cas 2 : avec nivellement de la production
Le calcul du pitch nécessite de comparer le temps nécessaire de production sur la journée (200x1+50x2+20x5=400 minutes) avec le temps requis (8h x 60 = 480min).
La différence correspond au temps que l’on pourra consacrer aux changements de série (80 min) que l’on compare à un temps de changement de série (10min) : 80/10 = 8 changements de série possibles par journée de production.
Il faudra donc produire chaque type de pièce chaque 1/8 jour, donc toutes les heures. C'est le picth de la boîte Heijunka.
Pitch = Période P x Temps de CO / (Temps requis sur la période P – temps total de production sur la période P)
Avec 1 pitch de 1 heure, le temps dévolu à la production est de 50 minutes (60 minutes – 10 minutes de C/O), soit :
- A = 50/1 = 50 produits soit 200/50 = 4 picths/jour
- B = 50/2 = 25 produits soit 50/25 = 2 pitchs/jour
- C = 50/5 = 10 produits soit 20/10 = 2 pitchs par jour
| Produits | 08h | 09h | 10h | 11h | 13h | 14h | 15h | 16h |
| A = 200 | 50 | 50 | 50 | 50 | ||||
| B = 50 | 25 | 25 | ||||||
| C = 20 | 10 |
10 |
Les en-cours sont ainsi limités à 50 unités et chaque produit est délivré plusieurs fois par jour (au minimum 2 fois/jour).
On remarque que comme pour le « kanban », plus les temps de changement de série sont faibles, plus les tailles de lot sont réduites et plus le pitch correspond à un laps de temps réduit.
Ainsi, dans cet exemple, si le temps de changement de série passe à 5 minutes, on pourra réduire le pitch à 30 minutes et niveler 2 fois plus la production.
EXEMPLE 2 : nivellement de ressources amont grâce à une boîte Heijunka
Soit un poste d’assemblage de 3 produits A,B et C différents faisant appel à la fabrication d’ébauches A’, B’ et C’ réalisées par des postes différents avec les temps de cycles suivants :
· TC1 (ébauches A’) = 10 minutes
· TC2 (ébauches B’) = 20 minutes
· TC3 (ébauches C’) = 40 minutes
L’usine est ouverte 16 jours par mois, 10h par jour avec 2x15 minutes de pause (soit 570 minutes/jour). La demande moyenne mensuelle de produits A, B et C est la suivante :
· A = 896 soit 56 unités/jour
· B = 464 soit 29 unités/jour TOTAL = 114 unités/jour donc : Takt Time (TT) = 570/114= 5 minutes
· C = 464 soit 29 unités/jour
Conformément aux règles d’équilibrage du Lean, le poste d’assemblage est ajusté pour avoir un temps de cycle de 5 minutes afin de répondre à la demande client.
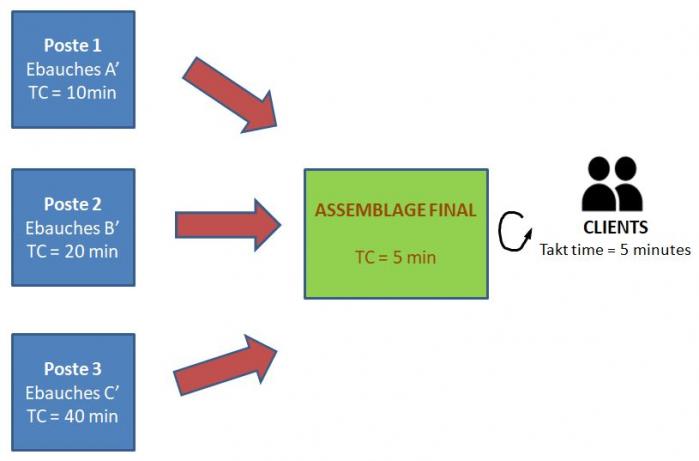
Cas 1 : sans nivellement de la production
Si chaque jour, tous les produits A sont réalisés puis tous les B et enfin tous les C, cela conduit à des vagues de travail en amont, nécessitant des pics de ressources :
· Poste 1 (ébauches A’) = TC/TT = 2 personnes employées pendant 4h40 puis inoccupées
· Poste 2 (ébauches B’) = TC/TT = 4 personnes employées pendant 2h25 puis inoccupées
· Poste 3 (ébauches C’) = TC/TT = 8 personnes employées pendant 2h25 puis inoccupées
Soit au total 14 personnes partiellement occupées au poste amont.
Cas 2 : avec nivellement de la production
Le pitch est ici impulsé par la demande client soit 5 minutes
(114 produits à assembler par jour avec un temps de cycle de 5min sans C/O = temps requis du poste d’assemblage).
En revanche, le prélèvement au niveau de chaque poste peut être ajusté afin de niveler la production sur toute la journée :
· Poste 1 (ébauches A’) = 570/56 ≈ 1 pièce toutes les 10 minutes (1 picth sur 2)
· Poste 2 (ébauches B’) = 570/29 ≈ 1 pièce toutes les 20 minutes (1 picth sur 4)
· Poste 3 (ébauches C’) = 570/29 = ≈ 1 pièce toutes les 20 minutes (1 picth sur 4)
Ce qui conduit à la boîte Heijunka suivante :
| Produits | 8h00 | 8h05 | 8h10 | 8h15 | 8h20 | 8h25 | 8h30 | 8h35 | 8h40 | 8h45 | 8h50 | 8h55 | 9h00 | ... |
| A | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||
| B | 1 | 1 | 1 | |||||||||||
| C | 1 | 1 | 1 |
Compte tenu d’un prélèvement d’ébauches plus régulier à chaque poste, les ressources nécessaires sont :
· Poste 1 (ébauches A’) = TC/10 = 1 personne employée à plein temps
· Poste 2 (ébauches B’) = TC/20 = 1 personnes employée à plein temps
· Poste 3 (ébauches C’) = TC/20 = 2 personnes employées à plein temps
Soit au total 4 personnes employées à plein temps au poste amont (donc 3,5 fois moins que sans le nivellement).
La boîte Heijunka permet ainsi d’éviter le gaspillage de ressources.
Le 24/09/2018
DDMRP : une méthode d’ordonnancement de la production tirée par la demande
Introduction
Le DDMRP, Demand Driven MRP ou « MRP piloté par la demande », est un outil d’ordonnancement de la production, qui a été détaillé en 2011 dans le livre « Orilcky’s Material Requirement Planning » écrit par Carol PTAK et Chad SMITH.
Le DDMRP a pour particularité de réhabiliter la notion de stocks, comme moyen permettant de dissocier la production de la demande.
Le DDMRP acte des défauts inhérents au modèle MRP : en effet, celui-ci a tendance à générer de nombreux stocks inutiles et donc des coûts importants. Cela résulte du fait que le MRP s’appuie sur une prévision plus ou moins juste de la demande (on estime que les meilleures entreprises atteignent une qualité de prévision de 75 à 80% par article par mois – autrement dit, qu’elles se trompent de 20 à 25% !) pour produire en « flux poussé » (accumulation de stock). Le MRP a également du mal à tenir compte des aléas de production, ainsi que de la variabilité des processus et de la demande.
Ainsi, le modèle MRP conduit à une répartition générale des articles dans l’usine oscillant entre « trop peu » et « trop », en fonction des variations de la demande. L’effet « coup de fouet » est un parfait exemple de cette oscillation, d’autant plus importante que l’on remonte vers l’amont de la Supply Chain, en réaction à une simple variation de la demande.
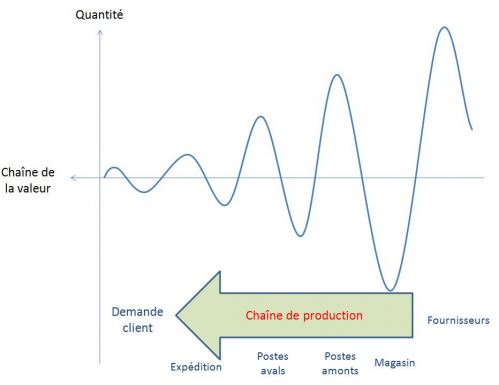
C’est en réaction à ces défauts que les démarches Lean, 6 sigma et théorie des contraintes se sont développées, avec pour point commun « une vision flux » de la production, suggérant d’abandonner le MRP pour l’ordonnancement quotidien de la production.
Le DDMRP combine ainsi ces trois méthodologies et les réconcilie avec le modèle MRP.
1) Le principe DDMRP
Le DDMRP vise à comprimer les cycles pour répondre à la demande client tout en absorbant les variabilités (aléas, variations de la demande) par la mise en place de buffers. Il a pour conséquence de tirer le flux de production de l’aval vers l’amont.
C’est un processus en 5 étapes.
1-Positionner les buffers
2-Dimensionner les buffers
3-Ajuster dynamiquement les buffers
4-Planifier les réapprovisionnements à partir de la demande réelle
5-Exécuter les ordres avec l'appui d’alertes paramétrées
Le MRP n’est cependant pas abandonné : en effet le processus, PIC/PDP reste valable pour prévoir le niveau des ressources. L’ordonnancement de la production suivant le DDMRP ne concerne que les articles aux points de commande stratégiques de la Supply Chain, les autres restants déterminés par la méthode classique MRP
Les approches Lean ou 6 sigma, ne sont pas non plus remises en cause par le DDMRP et restent totalement nécessaires à l’amélioration continue car, comme le montrent les règles de dimensionnement des buffers, ces derniers sont directement liés au délai de réapprovisionnement de fabrication et à la variabilité des processus. Donc plus on tend à les réduire, plus les buffers, et donc le stock moyen, sera faible.
2) Les 5 étapes DDMRP
2.1- Positionner les buffers
On commence par identifier les « points de commande » stratégiques qui ne permettent pas d’atteindre le cycle demandé par le marché et y positionner des buffers (ce sont finalement des stocks « virtuels ») qui vont raccourcir le cycle apparent et absorber la variabilité.
Ces buffers sont positionnés sur l’ensemble de la chaîne de production, de l’entrée matière à la livraison client. On les symbolise par le sigle suivant :

L’objectif est de découpler les étapes de production (ou boucles découplées) pour fiabiliser le flux.
Le « cycle découplé », pour chaque boucle découplée, correspond à la plus longue chaîne non protégée de la gamme permettant de satisfaire les besoins du marché (une fois les buffers mis en place). Il est caractérisé par un Lead Time correspondant au temps de traversée le plus long dans la nomenclature entre 2 points de découplage : on l’appelle l’ASR Lead Time (pour actively synchronized replenishment LT) ou DRAS en français.
Exemple : voici les buffers à positionner dans la nomenclature de production suivante avec une contrainte de délai de livraison client de 10 jours
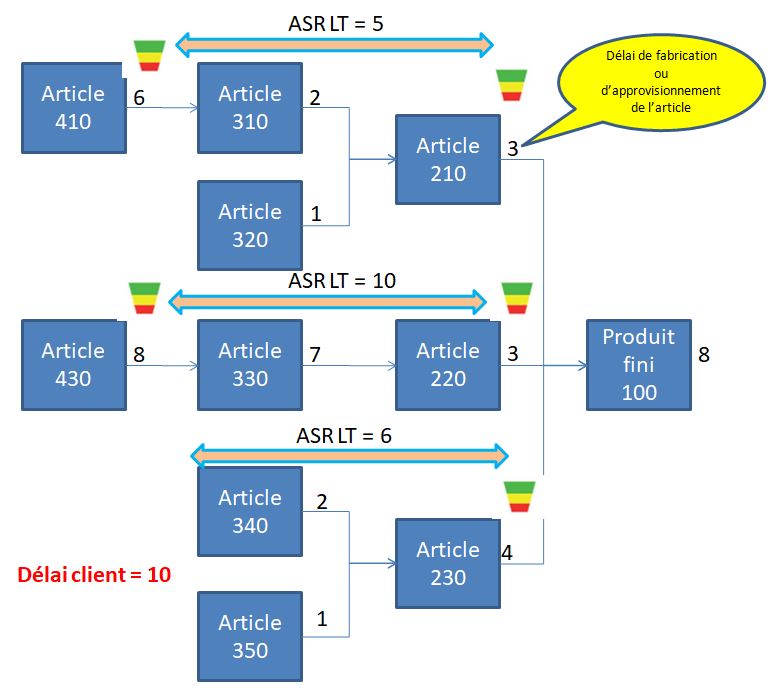
Voici les principaux critères pour sélectionner les points de commandes stratégiques où il est nécessaire de placer un buffer :
- Le délai de livraison exigé par le client ou imposé par le marché,
- La variabilité de la demande ou de la Supply Chain,
- La flexibilité des stocks,
- La structure de la Supply Chain (risque fournisseur par exemple),
- La protection des « goulots » (voir gestion de production selon la méthode DBR).
2.2- Dimensionner les buffers
Les buffers sont calculés en fonction de la consommation moyenne journalière (CMJ ou ADU = average daily usage - la CMJ est généralement calculé sur la base d'un historique des consommations sur un horizon de 6 mois), du temps cycle découplé de la boucle en amont du buffer (ASR LT) et de la variabilité (sur les délais ainsi que sur la demande).
Ils sont constitués de 3 zones. Le buffer total correspond à la somme de ces 3 zones. Nous retrouvons en commençant par la base du buffer :
- La zone ROUGE
Elle correspond au stock de sécurité et est dimensionnée comme suit :
Lead Time de la boucle (cycle découplé) x demande/consommation moyenne x facteur Lead Time
x (1 + facteur de variabilité volume)
Au sein de la zone rouge, on distingue une zone rouge de base qui correspond à la première partie de la formule (variabilité délai) sans multiplication par « (1 + facteur de variabilité volume) ». Cette seconde partie est appelée la zone rouge de sécurité : elle correspond à la sécurité à apporter pour cause de variabilité de la demande (risque externe).
> On retrouve dans cette formule la loi de Little : la zone rouge de base correspond ainsi à une fraction (% = facteur de Lead Time) de la quantité d’en-cours nécessaire au sein de la boucle pour tenir le débit journalier.
> Facteur Lead Time (ou facteur de délai de 0,2 à 0,7) : plus le cycle est court, plus le facteur de cycle Lead Time doit être grand : en effet, si le cycle découplé est très court, il faut beaucoup plus le protéger des petits aléas susceptibles d’avoir un impact relativement important sur le délai de commande.
> Facteur de variabilité en volume (de 0,2 à 0,75) : la variabilité en volume est relative à l’environnement de chaque production. Afin de l’appréhender pour chaque article relativement aux autres articles, il suffit de classer (diagramme de Pareto) tous les articles en fonction de leur CoV (coefficient de variabilité), i.e. le ratio écart-type de consommation / CMJ. Plus le CoV est élevé, plus le facteur de variabilité doit être important.
> Attention : le Lead Time de la boucle correspond bien au temps de traversée de la boucle (et non pas au temps de cycle du poste amont … même si dans certains cas, cela peut correspondre à la même valeur !).
.
- La zone JAUNE
Cette zone correspond à la quantité minimum prévue par la loi de Little pour tenir le temps de cycle en consommation « habituelle » augmentée de la marge pour variabilité et des aléas de délais (la zone rouge)
Elle est calculée comme suit :
Lead Time de la boucle (cycle découplé) x demande/consommation moyenne
- la zone VERTE
Il s’agit de la zone de production « normale » puisque dans cette zone on est au dessus de la quantité fixée par la loi de Little augmentée de la marge pour variabilité et aléas de délais (zone rouge + jaune).
On fixe une limite supérieure à la zone verte afin de garder une maîtrise du niveau de stock (le juste nécessaire).
Elle correspond au maximum entre les 2 valeurs suivantes :
· Lead Time de la boucle (cycle découplé) x Facteur Lead Time x demande/consommation moyenne
· Quantité minimale d’un ordre (MoQ / taille de lot)
Nota : Si la fréquence de passation de commande auprès du fournisseur est imposée (ex : commande 1 fois par semaine) et que celle-ci conduit à un en-cours théorique (pour notre exemple : 7 jours x CMJ) supérieur à la quantité calculée précédemment, c’est celle-ci qui sera retenue pour la zone verte.
On représente alors le buffer par un bar-chart intégrant les différentes zones définies au dessus.
Dans les calculs précédents, on veillera à convertir les Lead Time en jours (si les consommations moyennes sont bien des consommations journalières).
Exemple : Considérons l'artcile 220 dans la nomenclature présentée au §2.1avec les données suivantes :
- CMJ = 100 pièces / jour
- Taille de lot = 100
- Facteur de LT = 40%
- Facteur de variabilité de la demande = 50%
Compte tenu d'un ASR LT de 10 jours, le buffer DDMRP est alors défini comme suit (avec une zone rouge que l'on peut scinder en une zone rouge base de 400 pièces et une zone rouge de sécurité de 200 pièces) :
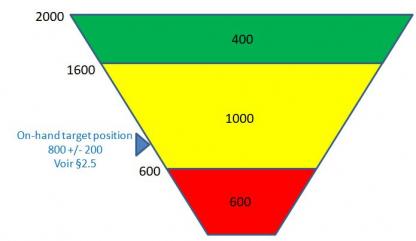
2.3- Ajuster dynamiquement les buffers
Il s’agit d’intégrer certains phénomènes temporels liés à l’activité de l’entreprise. On distingue plusieurs causes d’ajustements dynamiques :
· la saisonnalité,
· les promotions,
· les contraintes de capacités, et,
· les phases de lancement/obsolescence.
Pour ce faire, on affecte un coefficient d’ajustement à la consommation moyenne journalière.
Voici quelques exemples d’ajustements tirés d’une présentation de C. Ptak :
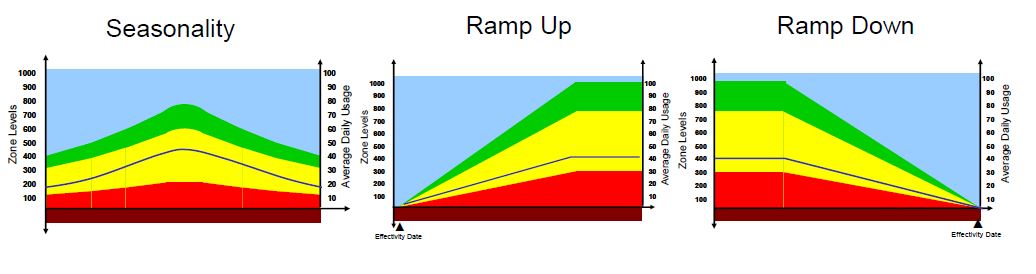
2.4- Planifier les réapprovisionnements à partir de la demande réelle
Le principe est de relancer l’approvisionnement dès que le « stock disponible » sort de la zone verte vers la zone jaune ou rouge : on planifiera alors un ordre de fabrication (en amont de la boucle correspondant au cycle découplé) permettant ainsi de revenir dans la zone verte.
La comparaison du stock disponible à l’échelle des buffers rouge/jaune/vert est réalisée quotidiennement et à chaque point de commande.
Le stock disponible est obtenu grâce à l’équation du flux disponible suivante :
Stock disponible (ou flux net) =
Stock réel disponible au buffer + En-cours de la boucle – Demande client qualifiée
- L’en-cours de la boucle correspond donc aux ordres de fabrications déjà lancés, et,
- La demande qualifiée correspond aux commandes fermes du jour + les pics. Les « pics » en langage « DDMRP » correspondent aux commandes fermes à venir ayant une quantité supérieure à la moitié de la zone rouge à l’intérieur du cycle découplé (ASR Lead Time).
On compare le résultat de l’équation de flux à l’échelle des buffers :
- Dans la zone Verte : pas de lancement d’OF ;
- Dans la zone Jaune : lancement d’OF pour une quantité permettant d’atteindre le top du vert (TOG = top of green);
- Dans la zone Rouge : lancement prioritaire d’OF pour une quantité permettant d’atteindre le top du vert (TOG = top of green);
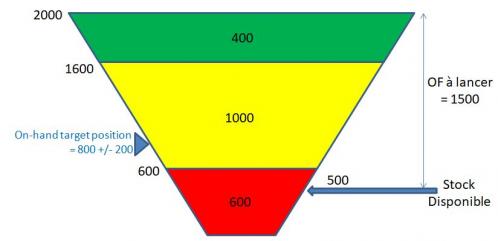
Exemple : considérons les données du jour suivantes pour l'article 220 de la nomenclature présentée au §2.1
- commande du jour = 80 pièces,
- stock physique = 500 pièces,
- en-cours physique = 400 pièces
- carnet de commandes fermes à 15 jours
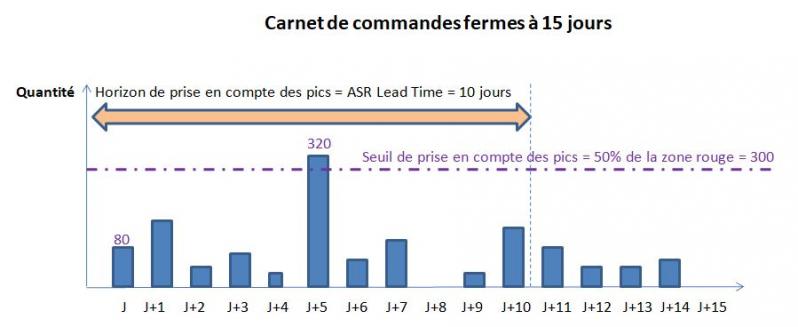
L'équation de flux indique le stock disponible : 400 + 500 - 80 - 320 (1 seul pic à prendre en compte) = 500 pièces. Ce niveau correspond à la zone rouge du buffer : il faut donc lancer en priorité un OF en amont de la boucle d'une quantité à produire de 1500 pièces.
Une schématisation de « type VSM » conduirait à présenter le pilotage DDMRP de cette boucle de la manière suivante :
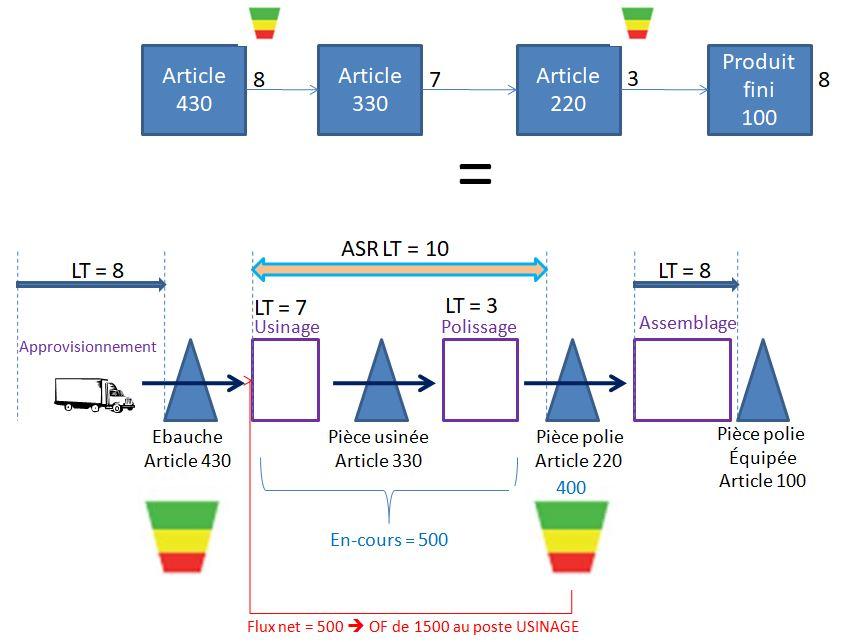
La différence avec le modèle MRP est que l’exécution des OF ne dépend plus d’une planification prévisionnelle de la demande, plus ou moins juste, mais du taux de remplissage d’un buffer en fonction de la demande réelle et de la quantité réelle circulant dans la boucle découplée (tenant compte des éventuels aléas que la production a subi).
Ainsi, la planification DDMRP va conduire à piloter un stock disponible entre la base de la zone verte et le top de la zone verte (lorsque la consommation est stable et sans pic) : le dimensionnement de la zone verte détermine donc la quantité moyenne de l’ordre de fabrication et sa fréquence de lancement (CMJ/zone verte - elle diminue lorsque la quantité moyenne augmente). On remarquera également que le rapport (buffer jaune / buffer vert) rend compte du nombre moyen d’OF ouverts dans l’en-cours.
Dans l’exemple étudié, cela conduit à maintenir un « en-cours + stock » de la boucle à 1600 pièces minimum (article 220) avec des OF moyens de 400 pièces, lancés tous les 4 jours soit 2,5 OF en moyenne dans l'en-cours. C'est ce que présente la simulation suivante du flux de la boucle étudiée avec une consommation constante de 100 pièces 220 par jour (sans pic):
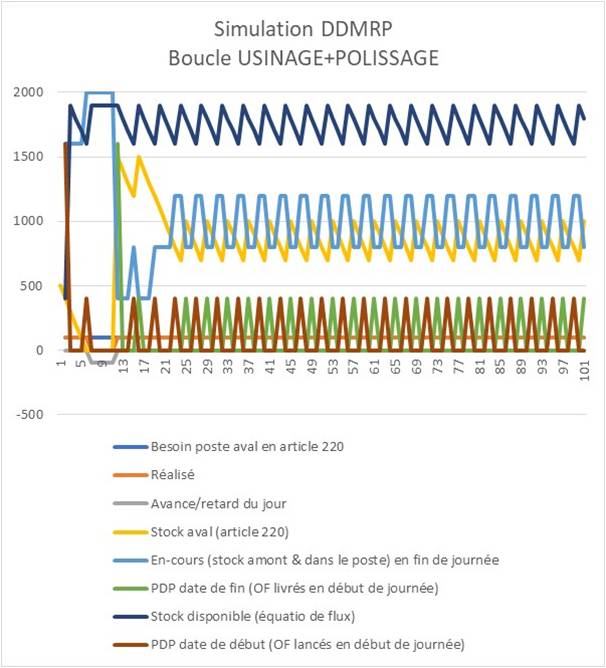
L’analyse de la formule du buffer « vert » montre que pour les pièces à long ASR Lead Time, le coefficient de lead time est faible ce qui indique une fréquence de recomplètement courte. Le DDMRP tend à créer artificiellement pour ces pièces, un système de livraison continue de type « convoyeur ».
2.5- Exécuter les ordres avec l'appui d’alertes paramétrées
L’exécution des ordres de fabrication est réalisée quotidiennement en fonction du résultat de l’équation de flux appliquée à chaque buffer. Afin d’avoir une vision synthétique et partagée du flux, on mettra en place un management visuel au travers 2 indicateurs :
- Les résultats de l’équation de flux disponible ;
- Le stock physique de l'article.
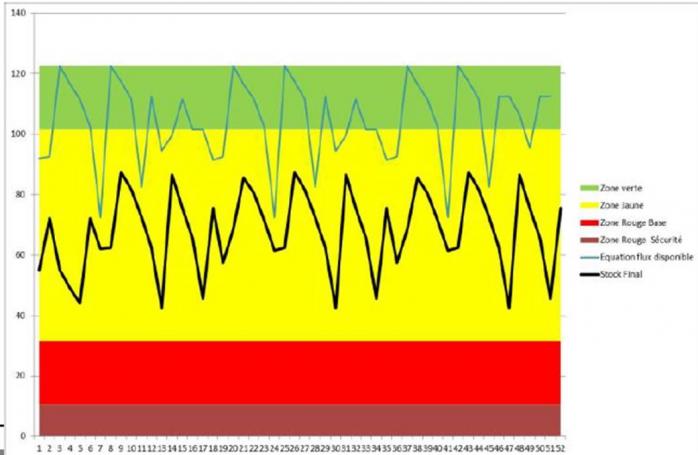
L’expérience montre que pour le stock physique de chaque artricle, la cible (appelée « on hand target position ») devrait correspondre à la zone rouge + la moitié de la zone verte. La zone d’évolution du stock devrait osciller autour de cette position +/- 50% de la zone verte.
Voir l'ensemble des billets du BLOG
Le 08/06/2018
Le SMED (single minute exchange of die), que l’on peut traduire par « changement de série en moins de 10 minutes » (donc en un temps en minutes correspondant à un seul digit) est une méthode de réduction des temps de changement de fabrication développée par S. Shingo dès les origines du TPS (Toyota Production System).
Pour les entreprises qui n’ont pas connu de révolution Lean, les tailles de lot correspondent aux quantités économiques calculées grâce à la formule de Wilson (issue du Fordisme). Ces tailles de lots importantes conduisent à une surproduction et aux nombreux gaspillages que cela entraîne :
· des stocks importants
o immobilisant de la trésorerie et augmentant le besoin en fond de roulement (ROI en baisse),
o engendrant des coûts (surfaces de stockage, inventaires, transport et déplacements inutiles, …),
o rendant plus difficile leur gestion (plus il y a de pièces moins on trouve celle dont on a réellement besoin),
o augmentant mécaniquement le temps de traversée de l’usine en application de la loi de Little (WIP = LT x débit),
· des problèmes qualité détectés tardivement et donc résolus tardivement après leur genèse,
· des produits susceptibles de n’être jamais vendus aux clients (puisque non commandés au moment de leur production),
· une flexibilité réduite vis-à-vis du client (en allongeant le Lead Time et donc la capacité de l’entreprise à s’adapter aux évolutions de la demande client).
Conscient de ces travers, Toyota a ainsi développé la technique SMED pour réduire les tailles de lot avec la finalité de fluidifier le flux de production.
Pour ce faire, il fallait trouver le moyen de réduire drastiquement les temps de changement de série qui contribuent directement au dimensionnement des tailles de lot.
Quantité économique = √ (2 x D x Ccs / Cp x Tps)
D = Débit de pièces par unité de temps
Ccs = Coût d’un changement de série
Cp = Coût d’une pièce
Tps = Taux de possession des stocks par unité de temps
Ainsi, l’application de la formule de Wilson indique qu’une réduction d’un facteur 2 du coût d’un changement de série permet de réduire d’un facteur √2 la taille de lot.
En visant un temps de changement de série idéal strictement inférieur à 10 minutes, S. Shingo avait l’objectif que pour une opération de production de 1h30 (90 minutes), le changement de fabrication représenterait ainsi 9 minutes ou moins (également appelée « règle du un pour dix » : les temps alloués au changement de série ne doivent pas dépasser 10% du temps de disponibilité des machines).
La mise en œuvre du SMED permet également de lisser la charge, en volume et mix produits, ce qui rend la production plus flexible aux évolutions de la demande client avec des niveaux de stocks intermédiaires de chaque référence plus faibles.
Par exemple, imaginons une usine ouverte 8h par jour et fabricant sur une seule machine 2 produits A et B avec un temps de cycle de 12s, une demande client de 500 unités de chaque produit et un temps de changement de série de 2h20.
L’organisation de la journée de travail est alors la suivante :

Si le temps de changement de série était divisé par deux, la production pourrait être lissé de telle manière que dès la mi-journée la moitié de la production journalière des 2 produits pourrait être mise à disposition du client avec l’organisation suivante :

Ainsi la finalité du SMED n’est pas de récupérer du temps improductif pour produire plus mais bien de fluidifier le flux de production en réduisant les tailles de lot et en nivelant la production en volume et mix produits. Il est, cependant, vrai que lorsque le SMED s’adresse à un goulot de production (voir théorie des contraintes), il pourra également être mis à profit pour gagner en capacité.
Vocabulaire anglais spécifique au 6 sigma
Le 07/06/2018
| English | Français |
| 7 points in row | 7 points d'affilée (tendance sur un carte de contrôle) |
| a boxplot (box-and-whisker diagram) | une boîte à moustache |
| a control chart | une carte de contrôle |
| a controllable factor (DOE) | un facteur contrôlé |
| a data collection planning | un plan de collecte des données |
| a design of experiments | un plan d'expériences |
| a dot plot | un diagramme des fréquences |
| a fishbone diagram | un diagramme en arête de poisson |
| a formula | une formule |
| a gate review (DMAIC) | la revue de fin d'étape |
| a lurking variable | une variable cachée |
| a main effect plot / interaction plot | un diagramme des effets / des intercations |
| a pairwise comparison (ex : Tukey) | une comparaison (des moyennes) deux à deux |
| a Pareto chart | un diagramme de PARETO |
| a ranked order set of data | des données ordonnées |
| a run (DOE) | un essai |
| a run / trial (DOE) | un essai |
| a sample | un echantillon |
| a scatter plot >> positive/négative/no correlation | un graphe des effets ( (Y = f(X1) - autres Xi fixés) |
| a survey | une enquête |
| a two-way / three-way interaction (DOE) | une interaction du 2ème/3ème ordre |
| an hypothesis testing | un test d'hypothèse |
| an outlier | un point aberrant |
| ANOVA assumptions : normal distribution - equal of variances | les pré-requis de l'ANOVA |
| cause-focused tools : 5 Whys - Fishbone diagram | outils d'analyse des causes : 5P - Ishikawa |
| Chi square | Khi2 |
| common cause /special or assignable cause | causes communes /spéciales |
| defective | défaillant - douteux |
| descriptive statistics | statistiques descriptives |
| df (degree of freedom) | ddl (degrés de liberté) |
| fractional-factorial DOE | plan fractionnaire |
| full DOE | plan complet |
| gage R&R | test R&R |
| in statistical control / out of control | sous contrôle statistique / hors contrôle |
| independent data | données indépendantes |
| inferential statistics | statistiques inférentielles |
| input variable / independent variable (X) | facteur X |
| linearity / accuracy / stability / discrimination | linéarité / précision / stabilité / discrimination |
| MSA (measurement system analysis) | analyse du système de mesure |
| noise factor (DOE) | facteurs bruits |
| normally distributed | distribuées suivant une Gaussienne |
| on one side of the average | d'un côté de la moyenne |
| one-way / two-way ANOVA | ANAVAR à un facteur / deux facteurs |
| output/response variable / dependent variable (Y) | caractéristique Y |
| paired / independent samples | échantillons apprairées / indépendantes |
| Pearson coefficient r (correlation) / r² is the percentage of variation in Y that is attributed to X | Coefficient de Pearson r / r² |
| random | aléatoire |
| regression : simple linear / multiple | régression : linéaire simple / multiple |
| reject / accept the null hypothesis | accepter / rejeter l'hypothèse nulle |
| repeatability & reproductibility | répétabilité & reproductibilité |
| short-term/lon-term capability | capabilité court/long-terme |
| skewed data | données assymétriques |
| steadily increasing / decreasing | en hausse / baisse constante |
| the 95% confidence interval | l'intervalle de confiance à 95% |
| the central limit theorem | le théorème central limite |
| the central tendancy / spread | la position / la dispersion |
| the confidence level = 1 - α | e niveau de confiance = 95% |
| the control limits | les limites de contrôle |
| the control limits (upper UCL / lower LCL) | les limites de contrôle (sup / inf) |
| the data display | la représentation es données |
| the histogram (frequency plot) | l'histogramme |
| the kurtosis | le coefficient d'applatissement |
| the levels of a factor | les modalités d'un facteur (ANOVA) ou niveaux (DOE) |
| the mean / the average | la moyenne |
| the median | la médiane |
| the null/alternative hypothesis | l'hypothèse nulle (H0) / alternative (H1) |
| the range | l'étendue |
| the S/N - signal to noise ratio | le rapport signal sur bruit |
| the sample size | la taille de l'échantillon |
| the sampling | l'échantillonnage |
| the spread | la dispersion |
| the standard deviation | l'écart-type |
| the sum of squares (SS) | la somme des carrés |
| the type of data (attribute or discrete/ continuous data) | le type de donnée (données discrètes / continues) |
| the variance (advantage : additive) | la variance |
| the variation | la variabilité |
| the who/what/where/when/how and why (five W et one H)- Is/Is'nt The last W is asked 5 times (the 5 why) |
QQOQCP / Est-N'est pas 5P (pourquoi) |
| α risk : probability to conclude there is a difference when there really isn't | risque alpha |
Le 26/03/2018
Les plans d'expérience (ou DOE - design of experiments en anglais) sont une méthode d’optimisation de la démarche expérimentale, vulgarisée dans le domaine industriel par le qualiticien japonais Génichi TAGUCHI, à partir des années 1960. Leur mise en œuvre est adaptée à l’optimisation du réglage des paramètres de multiples facteurs X contrôlés ayant une influence sur la qualité d’un produit (c’est le critère Y à minimiser, maximiser ou à cibler) tout en réduisant l’influence des facteurs non contrôlés (le bruit), difficiles ou trop coûteux à contrôler. Plutôt que d’éliminer ces facteurs bruits, il s’agit de trouver la combinaison des facteurs contrôlés rendant le produit « insensible » à ceux-ci.
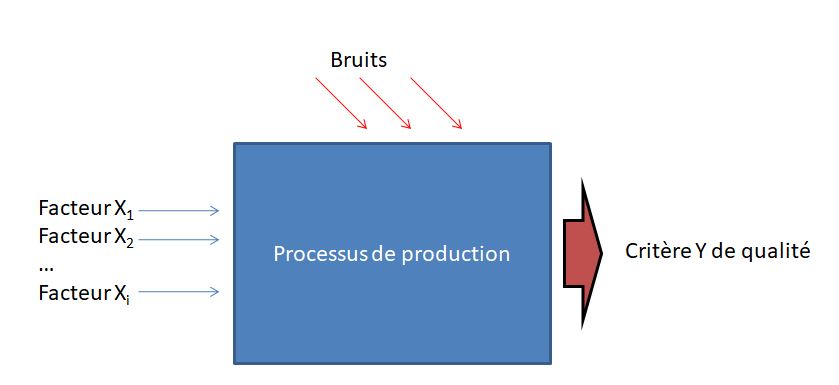
Dans une démarche 6 sigma, les plans d’expérience sont généralement mis en œuvre dans la phase « Improve » de la méthode DMAIC, c'est-à-dire lorsque l’on vise à déterminer la meilleure relation liant les X aux Y afin d’atteindre la qualité désirée (en réduisant la variabilité associée au processus de production).
Les plans d’expériences interviennent plutôt dans la phase de conception ou d’industrialisation d’un produit alors que la maîtrise statistique des procédés est plus pertinente en phase de production afin de contrôler et piloter la stabilité du processus de production.
Les plans d’expérience permettent de quantifier l’influence des facteurs X et de leurs interactions ainsi que d’identifier la meilleure combinaison de ceux-ci afin d’améliorer ou d’atteindre un niveau de qualité, tout en minimisant le nombre d’expérimentations à réaliser par une suite d’essais rigoureusement organisés.
Cela revient à rechercher les coefficients αi du polynôme suivant modélisant Y en fonction des X :
Y = α0 + α1 facteur X1 + α2 facteur X2 + α3 Interaction (facteur X1, facteur X2) + ….
La représentation graphique de cette fonction s’appelle la surface de réponse que l’on souhaite optimiser.
Une analyse de la variance (ANOVA) permet alors de conclure quant à la significativité de l’effet des facteurs et des interactions (avec un risque de première espèce de 5% d’affirmer que le facteur n’a pas d’influence alors qu’il en a effectivement une).
Pour bâtir un plan d’expérience, on retient pour chaque facteur un nombre fini de niveaux ayant une influence sur la qualité du produit, faisant ainsi l'hypothèse d'une linéarité de la réponse entre les niveaux. L’ensemble des combinaisons de niveaux de tous les facteurs conduirait à réaliser un nombre très élevé d’expériences (en tenant compte de la combinaison des facteurs), à répéter plusieurs fois pour accumuler des résultats statistiques, afin de tester leur influence sur le produit.
La force de la méthode TAGUCHI est :
- de limiter très fortement le nombre d’essais à réaliser en employant un plan factoriel pour lequel chaque niveau de chaque facteur est confronté à tous les niveaux des autres facteurs et dans des proportions égales (le plan est dit orthogonal),
- d’évaluer l’influence des facteurs non contrôlés (le bruit) sur l’effet des facteurs contrôlés.
Exemple : Avec 7 facteurs à 2 niveaux, il y a à 27 soit 128 combinaisons de facteurs alors que la matrice de Tagushi L8 (27) identifie 8 essais à réaliser !
Le plan d’expérience correspond donc aux essais à réaliser par combinaison de niveaux de facteurs : le plan est dit « complet » lorsqu’il intègre toutes les combinaisons de facteurs (dont les interactions entre facteurs) et « fractionnaire » lorsqu’il est restreint aux seuls facteurs sans tenir compte des interactions.
Chaque essai est répété plusieurs fois afin d’identifier la dispersion (bruit) autour du résultat de l’essai par rapport au critère mesuré, conséquence de l’influence des facteurs non contrôlés. On détermine alors pour chaque essai i, la moyenne Yi des effets et le rapport signal/bruit en dB (en fonction de la moyenne arithmétique des mesures et de leur dispersion) selon les formules développées par TAGUCHI.
Cas d’un critère à minimiser
S/Ni = - 10 * Log ([Σ yi2]/k) = -10 Log (σ²+Y²)
avec Y et σ, moyenne et écart-type des k répétitions de l’essai i
Cas d’un critère à maximiser
S/Ni = - 10 * Log ([Σ 1/yi2]/k) = -10 * Log ((1 + 3 σ²/Y2)/Y2)
avec Y et σ, moyenne et écart-type des k répétitions de l’essai i
Cas d’un critère à la valeur nominale (écart-type proportionnel à la position)
S/Ni = 10 log (Y2/σ²)
avec Y et σ, moyenne et écart-type des k répétitions de l’essai i
Cas d’un critère à la valeur nominale (écart-type indépendant de la position)
S/Ni = -10 log (σ² + (Y – Cible)2)
avec Y et σ, moyenne et écart-type des k répétitions de l’essai i
En faisant l’hypothèse que les effets moyens s’additionnent, on détermine ensuite la meilleure combinaison des facteurs comme étant celle pour laquelle leur effet va dans le sens de l’optimisation recherchée tout en maximisant le ratio signal/bruit.
Une fois les paramètres déterminés, on réalise un essai de validation des résultats obtenus. Afin de tester l'hypothèse de linéarité du modèle, on réalise cet essai de validation au centre du domaine d'étude (pour chaque facteur, on choisit le point médian entre les valeurs min et max). Si cet esssai est concluant (Y doit prendre la valeur moyenne de tous les essais, appelée T ci-dessous), on a alors trouvé la combinaison de facteur X répondant à l'objectif de qualité Y. Il ne reste plus qu'à l l'industrialiser.
Nombre minimal d'essais à réaliser
Le nombre minimal d'essais à réaliser pour étudier un système donné (plusieurs facteurs et interactions à des niveaux différents pour chaque facteur) est égal au nombre de degrés de libertés du système. Par exemple, pour l'étude du système suivant :
Y = α0 + α1 A (2 niveaux) + α2 B (3 niveaux) + α3 C (3 niveaux) + α4 AC
ddl =1 + 1 + 2 + 2 + 1 x 2 = 8
Il faudra effectuer au minimum 8 essais pour déterminer les coefficients αi.
La condition d'orthogonalité peut, cependant, conduire à un nombre d'essais supérieur au nombre de degrés de liberté. Cette condition d'orthogonalité indique en effet que le plan devra comporter un nombre d'essais multiple du PPCM du produit du nombre de niveaux de toutes les actions disjointes.
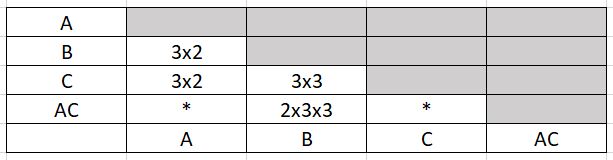
Dans cet exemple, le nombre minimal d'essais à réaliser pour respecter la condition d'orthogonalité est 2x3x3 soit 18 essais.
On comprend donc que pour minimiser le nombre d'essais il faut éviter de prendre des nombres de niveaux premiers entre eux et n'étudier des interactions disjointes que lorsque cela est indispensable.
Les tables de TAGUCHI
Elles se présentent sous forme de matrices Ln(Nk) présentant la configuration des essais à réaliser : en ligne les n essais à réaliser, en colonne les k facteurs ou combinaisons de facteurs avec en intersection les niveaux 1 à N à prendre en compte.
Pour un plan complet à f facteurs à 2 niveaux, la table à utiliser est la table Ln(2k) telle que n = 2f . Cette même table peut être utilisée comme plan fractionnaire pour étudier k facteurs sans interaction : chaque colonne est alors affectée à 1 facteur, étant entendu que certains facteurs sont confondus avec certaines interactions entre facteurs, considérées alors comme négligeables.
Les tables de TAGUCHI sont des plans fractionnaires astucieux qui prennent pour hypothèse que les interactions d'ordre 3 (1 facteur x 1 intéraction d'ordre entre 2 facteurs ou 1 intéraction à 3 facteurs) sont négligeables et que seules quelques interactions d'ordre 2 sont non nulles.
Elles sont accompagnées :
- d'un triangle des interactions, indiquant les numéros de colonne correspondant aux interactions entre 2 facteurs, et,
- d'un ou plusieurs graphes des effets, permettant de visualiser les différentes possibilités de mise en oeuvre de la matrice en fonction des interactions à étudier. Ces graphes indiquent également quelles colonnes doivent être affectées aux facteurs les plus difficiles à modifier au cours des expérimentations.
Les 18 tables orthogonales de TAGUCHI, classées en fonction de la possibilité ou non d’étudier des interactions, sont répertoriées ici :

Détaillons, par exemple, la table L4(23).
| N° essai / N° de colonne | 1 | 2 | 3 |
| 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 2 |
| 3 | 2 | 1 | 2 |
| 4 | 2 | 2 | 1 |
(en intersection de chaque ligne/colonne, on note le niveau 1 ou 2 à adopter pour chaque facteur dans le cadre de l'essai considéré)
-accompagnée du triangle des interactions :
| 2 | 3 | |
| (1) | 3 | 2 |
| (2) | 1 |
-et du graphe des effets :
![]()
Cette table est utilisée :
- Soit pour un plan complet à 2 facteurs A et B (facteur A en colonne 1, facteur B en colonne 2 et intéraction A/B en colonne 3)
- Soit pour un plan fractionnaire à 3 facteurs A,B,C sans tenir compte d’interactions ou plus exactement avec l’éventuelle interaction AB cumulée avec l’effet du facteur C (en colonne 3). On dit que les deux actions sont des alias. La résolution du plan fractionnaire est d’ordre III (1 facteur au moins confondu avec une interaction d’ordre II)
Si cette interaction ne peut pas être négligée, il faudra étudier séparément cette interaction et le facteur C ; pour ce faire, il faudra utiliser un plan complet à 3 facteurs L8 : on dit que l’on « désaliasse » le plan fractionnaire. L’utilisation d’un plan fractionnaire peut conduire à de lourdes erreurs si on néglige des interactions significatives.
On cherche à optimiser la surface de réponse du polynôme suivant :
Y = α0 + α1 A + α2 B + α3 A x B (2 facteurs + 1 interaction)
Ou
Y = α0 + α1 A + α2 B + α3 C (3 facteurs – interactions nulles)
Afin de pouvoir comparer les αi, , on utilise une unité standard, appelée notation de Yates, pour tous les facteurs de -1 (niveau mini) à +1 (niveau maxi).
Les résultats des 4 essais, prescrits par la table et répétés n fois, sont consignés dans le tableau suivant :
(exemple: 2 facteurs A et B + 1 interaction A/B - critère Y à minimiser) :
| Moyenne |
S/N = - 10 * Log (1/n * Σ Yk2) |
||
| Essai 1 | Y11 | S/N(Y11) | |
| Essai 2 | Y12 | S/N(Y12) | |
| Essai 3 | Y21 | S/N(Y21) | |
| Essai 4 | Y22 | S/N(Y22) |
On note :
- Xi la moyenne des résultats lorsque le facteur X est de niveau i, et,
- T la moyenne des résultats de tous les essais de la matrice de Tagushi (moyenne du plan) = (Y11 + Y12 +Y21+Y22) / 4
On montre que :
- Effet (Xi) = Xi – T → par exemple : Effet (A1) = (Y11+Y12)/2 - T.
On note que ∑ Effet (Xi) = 0. On dit que le facteur Xi a (N-1) degrés de libertés, c'est à dire qu'il suffit de calculer (N-1) effets pour connaître tous les effets du facteur X.
- Effet (Interaction XiYj) = XiYj– Effet (Xi) – Effet (Yj) – T → par exemple : Effet (A1;B2) = Y12 - Effet(A1) - Effet(A2) - T
On note que ∑ Effet (XiYj) à i fixé = 0. L'intéraction XiYj comporte (N-1) x (N'-1) degrés de libertés.
alors : α0 = T ; αi = Effet (X2 ou Interaction X2Y2)
Les effets doivent être calculés sur les valeurs brutes Y et sur les valeurs signal/bruit S/N(Y) car les facteurs peuvent avoir une influence ou non sur les unes et/ou les autres. Le calcul des αi permet d'établir les graphes des facteurs et les graphes des interactions, représentant la dépendance supposée linéaire de chaque effet/facteur sur la plage normalisée [-1;1].
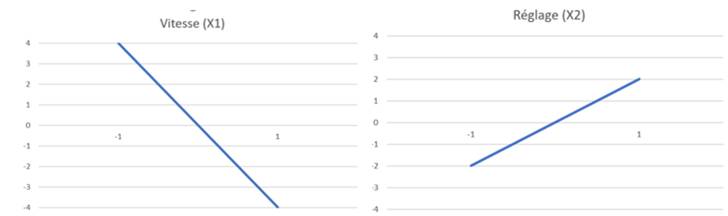
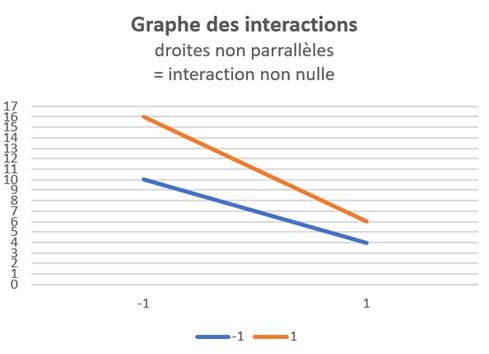
La significativité des effets peut être établie grâce à une analyse de la variance ou ANOVA (effet significatif si F > Flimite):
|
|
A |
B |
AxB |
Résidus |
TOTAL |
|
SS |
nx4xEffet(A1)² |
nx4xEffet(B1)² |
nx4xEffet(A1xB1)² |
Total-SSA-SSB-SSAxB |
∑(nx4)(Yk-T)² |
|
ddl |
1 |
1 |
1 |
nx4-1-3 |
nx4-1 |
|
V |
SSA/ddl |
SSB/ddl |
SSAxB/ddl |
Rv=SSR/ddl |
SST/ddl |
|
F |
VA/Rv |
VB/Rv |
VAxB/Rv |
|
|
|
Contribution |
SSA/SST |
SSB/SST |
SSC/SST |
|
|
|
Flimite à 5% |
Table Fisher-Snedecor (1 ; nx4-1-3) |
|
|
||
On détermine alors la meilleure combinaison des facteurs A (-1 ou +1) et B (-1 ou +1) comme étant celle pour laquelle leur effet va dans le sens de minimiser l'équation Y = α0 + α1 A + α2 B + α3
Le concept de capabilités en 6-sigma
Le 07/12/2016
La capabilité sert à quantifier l’aptitude d’un processus (compte tenu de ses limites naturelles) à produire à l’intérieur d’un intervalle de tolérance. L’étude des capabilités consiste à analyser l’adéquation des performances du moyen de production et son évolution dans le temps, par rapport à l’objectif de performance visé (valeur cible et intervalle de tolérance).
On distingue:
· La capabilité court-terme du processus, Cp, qui compare la dispersion naturelle du processus (sans action de causes spéciales) et l’intervalle de tolérance (IT): Cp = IT / 6σCT. C’est donc la capabilité du moyen de production si l’on arrive à stabiliser le moyen, c'est-à-dire à éliminer les causes spéciales occasionnant un étalement de sa dispersion.
· La performance long-terme du processus, Pp, qui prend en compte sur l’ensemble de population l’action des causes spéciales (occasionnant une dérive de la position moyenne du processus): Pp = IT / 6σLT. Elle traduit la qualité des produits livrés au client.
Cp et Pp vérifient: Pp ≤ Cp
On définit également un indicateur de déréglage long-terme, Ppk, ratio de la distance entre la moyenne sur toute la population (μ) et la limite de tolérance la plus proche (TS ou TI), divisée par 3 σLT: Pp = (μ-T)/3σLT.
Un processus est dit capable sur le long terme, c'est-à-dire susceptible de ne pas produire de pièces défectueuses, si Ppk > 1,33 (i.e., moins de 64 pièces défectueuses par million pour un processus centré tel que Ppk=Pp=1,33).
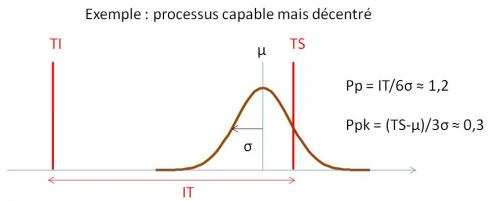
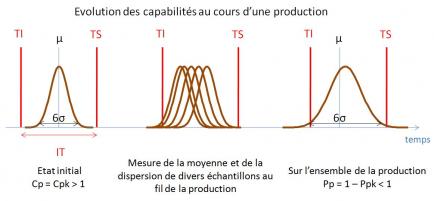
Ainsi, un processus part d’un potentiel de capabilité égal à Cp. La chute de capabilité de Cp à Pp traduit l’instabilité du processus (c'est-à-dire l’étalement de sa dispersion avec le temps parce que la machine ne tient pas la consigne sur la valeur cible et que ces écarts ne sont pas corrigés) alors que la chute de capabilité de Pp à Ppk est due au déréglage du processus sur le long terme (écart de la moyenne par rapport à la cible).
L’étude de cette « chute des capabilités » est un outil puissant de l’approche 6-sigma pour améliorer très sensiblement le taux de qualité d’un processus de production.
Le 27/11/2016
L'analyse de déroulement (AD) ou analyse en profondeur de processus (APP) est une analyse chronologique de processus, plus détaillée qu’une VSM et sur un périmètre plus restreint, visant à identifier de manière exhaustive les différentes étapes de réalisation du processus.
La méthodologie de l’analyse de déroulement peut également être mise en œuvre pour réaliser une analyse de poste de travail : il ne s’agit plus de suivre les étapes d’un processus mais les tâches, dans un ordre chronologique, réalisées par un opérateur pour réaliser une gamme de travail.
L’analyse de déroulement a pour objectif de déterminer et d'améliorer l’efficience du processus actuel en catégorisant chacune des étapes en tâche à valeur ajoutée (VA) ou à non valeur ajoutée (NVA).
L’analyse de déroulement est standardisée par l’utilisation des symboles suivants pour qualifier les étapes constitutives du processus :
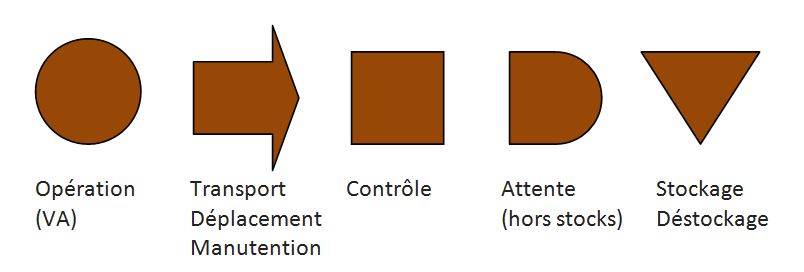
Les quatre derniers symboles sont dédiés aux étapes à non valeur ajoutée.
Ces symboles sont utilisés à la fois pour établir le graphique de flux (enchaînement des tâches) et la matrice de déroulement (quantifiant les temps dédiés à chaque étape mais aussi les distances parcourues, les quantités de matière transformées, les poids en jeu et le nombre d’opérateurs impactés).
En fin d’analyse du processus actuel, on définit les paramètres suivants que l’analyse de déroulement vise à améliorer :
· Efficacité du processus = nbr étapes à VA / nbr étapes VA + NVA
· Temps de traversée du processus = ∑ VA + NVA (temps) = LT
· Efficience du processus = ∑ VA (temps) / LT
· Indice de tension du flux = 1 / Efficience
L’amélioration du processus consiste à imaginer les actions à conduire pour simplifier le processus en éliminant les gaspillages qui le polluent. Pour ce faire, chaque étape est analysée afin d’évaluer s’il est pertinent de l’éliminer, de la combiner ou permuter avec une autre étape ou encore de la simplifier.
On construit alors le processus futur avec les symboles ci-dessus et on détermine les ratios d’amélioration des paramètres présentés plus haut.
L’analyse de déroulement peut être complétée par un diagramme Spaghetti afin de visualiser graphiquement les déplacements nécessaires à la réalisation du processus (mouvements de matière et/ou d’opérateurs) : celui-ci pourra servir à imaginer une nouvelle implantation du processus de production participant à la simplification du flux.
Le taux de rendement synthétique (TRS)
Le 08/11/2016
Le taux de rendement synthétique (TRS) ou OEE (overall equipement efficiency) mesure le rendement d’un moyen de production, d’une cellule voire même d’une chaîne complète.
Cet indicateur de productivité, au coeur des attentions de la démarche TPM (Total Productive Maintenance) permet non seulement de tracer et quantifier l’efficience d’une machine mais également d’identifier les axes d'amélioration pour faire progresser la productivité du moyen. Il est défini par la norme AFNOR NF E60-182.
TRS = nombre de pièces conformes produites / nombre de pièce théoriquement réalisables pendant le temps requis
(temsp requis = temps de mise à disposition de la machine pour produire)
On appelle « non-TRS » le complément entre le TRS et 100% : le non-TRS représente la capacité installée non utilisée pour produire ; c’est un gaspillage que le Lean vise à supprimer.
On peut faire apparaître dans l’égalité précédente des facteurs intermédiaires :
TRS = Taux de qualité (Tq) x Taux de performance (Tp) x Disponibilité opérationnelle (Do)
Avec :
· Tqualité = Nombre de pièces conformes produites / Nombre total de pièces effectivement produites.
Le taux de qualité peut être déduit des facteurs Cp et Cpk (leur combinaison permet, en effet, de calculer la probabilité DPMO de produire en dehors des tolérances : Tqualité = 1 – DPMO x 10-6)
· Tperformance = Nombre total de pièces effectivement produites / Nombre de pièces qui auraient dues être produites pendant le temps consacré à la production
· Disponibilité opérationnelle (Do) = Nombre de pièces qui auraient dues être produites pendant le temps consacré à la production / Nombre de pièces théoriquement réalisables pendant le temps requis
Le TRS est donc la combinaison de 3 taux inférieurs à 1 : il est donc toujours inférieur au taux le plus faible qui le compose. Les ordres de grandeurs cible sont les suivants :
- Perte de qualité < 1 % (Tq = 99,9%)
- Perte de disponibilité <10 % (Do = 90%)
- Perte de performance/efficacité < 5 % (Tp = 95%)
soit un TRS > 85 %.
Ainsi améliorer la productivité d’un moyen consiste à réduire les pertes de TRS en s’attaquant à chacun des 3 ratios participant au TRS :
· Tqualité : chantier 5S, chantier de déploiement de la MSP (cartes de contrôle et analyse de la chute des capabilités)
· Tperformance = chantier auto-maintenance, chantier 5S
· Do = chantier TPM, chantier SMED, management visuel
Les 3 taux composant le TRS peuvent être exprimés en ratio de temps plutôt qu'en ratio de pièces :
· Disponibilité opérationnelle (Do) = Temps de fonctionnement de la machine / Temps requis
avec : Temps de fonctionnement de la machine = Temps requis - ∑ arrêts (propres et induits)
et Temps requis = nombre de pièces théoriquement réalisables x TC théorique
La disponibilité opérationnelle peut également être calculée grâce aux indicateurs de maintenance MTBF (moyenne de temps de bon fonctionnement) et MTA (moyenne des temps d'arrêts propres et induits ) : Do = MTBF / (MTBF + MTA)
avec MTBF = ∑ temps de bon fonctionnement / nombre de périodes de bon fonctionnement (entre 2 arrêts)
· Tperformance = Temps net de production / Temps de fonctionnement de la machine
avec : Temps net de production = Nombre total de pièces effectivement produites x TC théorique = Temps réel de production x (TC théorique / TC réel)
· Tqualité = Temps utile de production sans défaut / Temps net de production
où Temps utile de production = Nombre de pièces effectivement produiconformes x TC théorique
NB : Le temps utile ne correspond donc pas au temps réel passé pour réaliser les pièces conformes (qui ferait intervenir TC réel)
Si le temps de mise à disposition de la machine (appelé temps requis) ne correspond pas au temps d'ouverture, on peut calculer de manière différenciée un TRS (par rapport au temps de mise à disposition = temps requis) et un TRG (par rapport au temps d'ouverture). Cela peut se produire en particulier lorsque l'usine est en surcapacité (par rapport à la demande du marché : on contraint la production sur un temps requis plus faible afin de ne pas produire de gaspillage (en surproduisant).
TRG = TRS x TR/TO
On parle également de TRE (taux de rendement économique) lorsque le calcul est réalisé sur un temps théorique d'ouverture de 24H/jour (point de vue économique).
TRE = TRG x TO/TT
On a donc toujours : TRS ≥ TRG ≥ TRE
Ces ratios sont souvent résumés par le schéma ci-après :

On comprend ainsi qu’améliorer le TRS consiste à réduire l’ensemble des pertes qui ont pour conséquence de réduire le temps requis au temps utile. La TPM classe ces pertes en 6 catégories :
Pertes participant au taux de disponibilité
- les arrêts propres fonctionnels (pannes supérieurs à 10 minutes)
- les arrêts d'exploitation (changement de série, d'outils,réglages, contrôles)
- les arrêts induits (manque de pièces ou de ressources, défaut d'énergie,...)
Pertes participant au taux de performance
- les micro-arrêts
- les ralentissement et marches à vide
Pertes participant au taux de qualité
- les défauts de qualité
- les pertes (qualité) au démarrage
On passe de la vision « nombre de pièces » à la vision « temps » en multipliant le numérateur et le dénominateur de la première égalité définissant le TRS par le temps de cycle théorique (ou de référence) de la machine :
TRS = TU / TR
avec
· TU = nombre de pièces conformes x TC théorique
· TR = nombre de pièces théoriquement réalisables x TC théorique
Le suivi du TRS d’une machine peut être réalisé manuellement ou par l’intermédiaire d’une solution informatisée au sein d'un MES (manufacturing execution system). Le suivi manuel consiste :
- à relever à intervalle de temps régulier (le pas est à adapter en fonction du TC) l'état de la machine et à affecter un code d'arrêt spécifique lorsque la machine ne produit pas, et,
- à relever le nombre de pièces produites dont le nombre de pièces non conformes.

Le calcul du TRS ne pose pas de grandes difficultés si l’on connait le TCthéorique, le temps d’ouverture (ou plus précisément le temps requis) et que l’on compte le nombre de pièces produites conformes aux spécifications sur une durée suffisamment représentative :
TRS = nombre de pièces conformes pendant le temps requis / (temps requis/ TCthéorique)
Exemple : Usine ouverte 8h/jour avec 2 x 10 minutes de pause – TC = 10’’ – nombre de pièces conforme en fin de journée : 2200 soit TRS = 2200 / (460’ x 60’’/10’’) ≈ 80%
Il est, en revanche, souvent beaucoup plus difficile d'évaluer les 3 ratios composant le TRS alors qu’ils sont indispensables pour décider des mesures d’amélioration pertinentes à conduire. Il peut alors être intéressant d’approcher ceux-ci par une estimation des causes de non-TRS exprimées en temps (sur une période suffisamment représentative de la production comme la journée ou la semaine) en distinguant les diverses cause de sous-performance : temps de panne, temps d’attente de personnels, temps de changement de série, autres temps d’attente, temps de réglage … Un diagramme de Pareto de ces causes permet alors de hiérarchiser les causes de sous-performance.
Le TRS est également utile en équilibrage de ligne de production ou pour le calcul du nombre de cartes Kanban car il permet de passer du TCthéorique au TCapparent compte tenu des pertes de disponibilité (pannes), de performance (écarts de cadence) et de qualité (tri des rebuts) : TCapparent = TCthéorique / TRS.
Le ratio entre le TCthéorique et le TCréel résultant des écarts de cadence ou sosu-vitesses est appelé le taux d'allure. Il vérifie :
Tp = Taux d'allure x TCréel x Nbr de pièces réellement produites / TR
Le TRS d'une ligne de production composée de plusieurs machines de taux de rendement synthétique TRSi (Tqi , Tpi et Doi) est donné par :
TRS = Do x Tp x Tq
avec :
- Tq = ∏ Tqi
- Tp = ∏ Tpi
- Do= 1 / (∑ 1/Doi - (n-1)) - si les valeurs de Doi sont proches de 1, Do = ∏ Doi
Voir l'ensemble des billets du Blog
